分步乘法计数原理可视作分类加法计数原理的运算简化

前言：本文是作者复习高中数学选修三课本时的思考题作答，内容浅显，仅作练笔。

1 乘法

乘法运算是特定条件下加法运算的简化。乘法（Multiplication），是将相同的数加起来的快捷方式。乘法的定义是：

求n个相同数a相加的运算，表示为

n \times a = \sum_{i=1}^{n}a（1）

或者，我们可以对定义的符号进行替换，这样做的目的是表明乘法不具有顺序性，即乘法结合律：

求a个相同数b相加的运算，表示为：

a \times b = \sum_{i=1}^{a} b = b \times a（2）

式(2)的符号替换将在后文被再次提到。

2 分类加法计数原理

分类加法计数原理可做如下定义：完成一件事有两类不同方案，在第1类方案中有m种不同的方法，在第2类方案中有n种不同的方法，那么完成这件事共有

N = m + n

种不同的方法。

例如，用一个大写英文字母或一个阿拉伯数字为教室中的座位编码，则因为大写英文字母一共有26种选择，阿拉伯数字一共有10种选择，所以总共能够编码26+10=36个座位。

3 分步乘法计数原理

分步乘法计数原理可做如下定义：完成一件事需要两个不同步骤，做第1个步骤时有m种不同的方法m_i，做第2个步骤时有n种不同的方法n_j，那么完成这件事共有

N = m \times n

种不同的方法。

例如，用一个大写英文字母和一个阿拉伯数字为教室的座位编码，其中字母在前，数字在后，共同组成两位编码。那么，因为大写英文字母一共有26种选择，阿拉伯数字一共有10种选择，所以总共能够编码26 × 10 = 260个座位。

4 两种计数原理的联系

对前述定义进行归纳，可以发现：在适用于分步乘法计数原理的问题中，对于每一个方法m_i，都有相同数量的n个方法n_j与之对应，如下图1。因此，对于每一个从m_i到n_j的过程，都类同于应用了一次分类加法计数原理，因为，两个步骤中的方法相互独立。而分步乘法计数的结果正是相当于每一种分类加法计数结果的合并，它简化了将不同分类加法计数结果相加的重复操作，而采用相乘的方式实现。不同的是，适用于分步乘法计数的问题规定了“步骤”，即先需要完成第1步中的某个方法m_i，才能去完成第2步中的方法n_j。

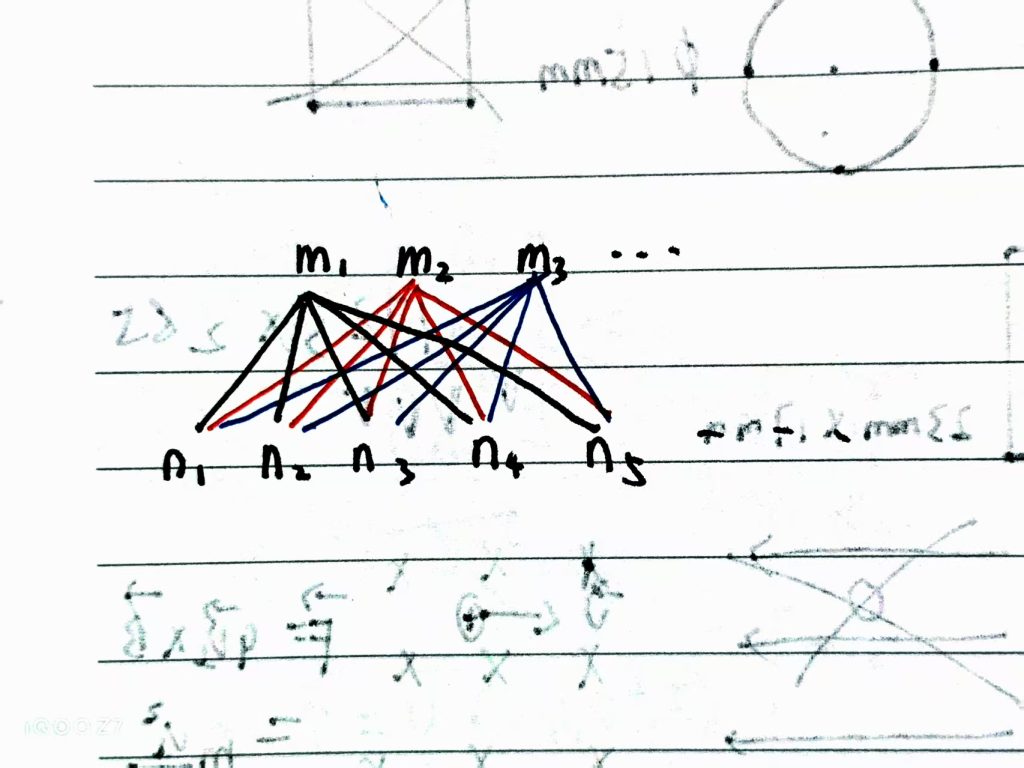
按照上述分析，我们可以发现，这一“合并”动作与乘法运算不谋而合。方法m_i的个数即是公式(2)中的a，方法n_j的个数即是公式(2)中的b，则为了统计完成这一件事的两个步骤可以有多少种不同的方案，我们计算：

a \times b = N